Sea R el pago periódico de una anualidad ordinaria, i la tasa de interés por periodo de interés, n el número de intervalos de pago (igual al número de periodos de interés por ser una anualidad ordinaria) y V el valor final de dicha anualidad.

· El primer pago R se convertirá en R (1 + i )^{n - 1}, puesto que está invertido durante (n - 1) periodos de interés.

· El segundo pago R, se convertirá en R (1 + i )^{n - 2}

· El penúltimo pago se convertirá en R (1 + i )¹

· El último pago será R.

· El valor final será:

V = R + R (1 + i ) + R (1 + i )² + ... + R (1 + i )^{n - 2} + R (1 + i )^{n - 1}

Como puede observarse, se ha obtenido la suma de n términos de una progresión geométrica de razón (1 + i ) y término inicial, R.

Aplicando la fórmula de la suma de los n primeros términos de una progresión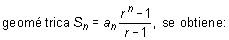

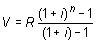
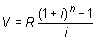
Ejercicio: cálculo del valor final de una anualidad ordinaria

 ¿En cuánto se convierte una anualidad ordinaria de 5 000 PTA anuales, durante 6 años, al 3 %?

Resolución:

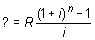
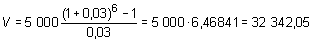
‚ Al final de cada año se depositan en el banco 150 000 PTA. Si el banco paga el 7 % anual, ¿cuánto dinero habría inmediatamente después del 5.º año? ¿Y después del 8.º?

Resolución:

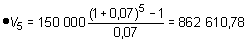
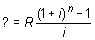
Al final del 5.º año habría 862 611 pesetas.

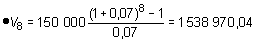
Al final del 8.º año habría 1 538 970 pesetas.

Clic aquí para descargar tu Certificado!