|
Sea C un capital invertido durante n años a una tasa i de interés compuesto por cada año.
Durante el primer año el capital C produce un interés I1 = C · i . El capital final será:
C1 = C + Ci = C(1 + i)
Después del segundo año, el capital C1 produce un interés I2 = C(1+i )·i = C(i + i 2). El capital final C2 será:
C2 = C1 + I2 = C (1 + i ) + C (i + i 2) = C (i 2 + 2i + 1) =
= C · (1 + i )2
Al cabo de n años el capital inicial C, invertido en la modalidad de interés compuesto se convertirá en un capital final Cn
Cn = C (1 + i )n
Puesto que el interés es la diferencia entre el capital final y el inicial:
I = Cn - C = C (1 + i )n - C, y sacando factor común C:
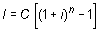
La tasa de interés se obtiene despejando en la fórmula de Cn:
Cn = C (1 + i )n
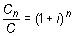
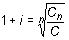
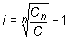
Aunque la fórmula del interés compuesto se ha deducido para una tasa de interés anual durante n años, todo sigue siendo válido si los periodos de conversión son semestres, trimestres, días, etc., sin más que convertir éstos a años:
· Si los periodos de conversión son semestrales,
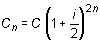
· Si los periodos de conversión son trimestrales,
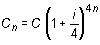
Ejercicio: aplicación de la fórmula del interés compuesto
Averiguar en qué se convierte un capital de 1 200 000 PTA al cabo de 5 años, y a una tasa de interés compuesto anual del 8 %.
Resolución:
· Aplicando la fórmula Cn = C (1 + i )n
? = C( 1 + i )n
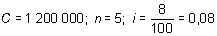
C5 = 1 200 000 (1 + 0,08)5 = 1 200 000 · 1,4693280 = 1 763 193,6
El capital final es de 1 763 194 PTA.
‚ Un cierto capital invertido durante 7 años a una tasa de interés compuesto anual del 10 % se ha convertido en 1 583 945 PTA. Calcular el capital inicial, sabiendo que los intereses se han pagado semestralmente.
Resolución:
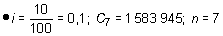
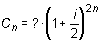
· Como los intereses se han pagado semestralmente, la fórmula que se ha de aplicar es:
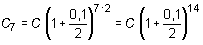
1 583 945 = C (1 + 0,05)14
1 583 945 = C · 1,97993160, y despejando C:
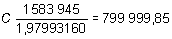
El capital inicial fue de 800 000 pesetas.
ƒ Calcular la tasa de interés compuesto anual que se ha aplicado a un capital de 1 500 000 PTA para que al cabo de 4 años se haya convertido en 2 360 279 PTA.
Resolución:
· Cn = 2 360 279; C = 1 500 000; n = 4
2 360 279 = 1 500 000 (1 + i )4
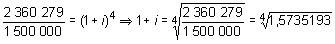
1 + i = 1,1199999
i = 1,1199999 - 1 = +0,1199999  0,12 0,12
La tasa de interés ha sido del 12 %.
|



