|
Un gráfico de control es una carta o diagrama especialmente preparado donde se van anotando los valores sucesivos de la característica de calidad que se está controlando. Los datos se registran durante el funcionamiento del proceso de fabricación y a medida que se obtienen.
Existen diversas preferencias técnicas para el establecimiento de la tolerancia y los límites de las especificaciones. Aunque en algunos casos los límites se han fijado de forma arbitraria, la mayoría de las veces, se han determinado cuidadosamente por medio de pruebas y se basan en experiencias con los materiales y los procesos de manufactura. Posteriormente, se trasladan a las hojas de tolerancias prácticas del talles. El gráfico de control tiene una línea central que representa el promedio histórico de la característica que se esta controlando y los límites superior e inferior que también se calculan con datos históricos. Por ejemplo, el personal de una planta ha agrupado intuitivamente las variaciones de las piezas manufacturadas, en dos categorías:
- Variaciones normales. Estas se refieren al total de la desviación que el obrero ya conoce que se debe presentar. Por ejemplo, a lo ancho de las telas no son totalmente aprovechables, ya que generalmente están perforadas a un centímetro de la orilla por los procesos de tintorería y acabados de la misma tela. Por lo tanto, si la tela tiene 150cm de ancho, la tolerancia normal será de 0.0133 centímetros.
- Variaciones anormales. Equivalen a una desviación mayor que la que el obrero experimentado sabe que se tiene que aceptar.
En los análisis de estas variaciones se basan las formas más usadas de las gráfica de control (hora a hora, día a día) de las características de calidad reales del producto (parte o unidad) con los límites que reflejan la capacidad de producir, de acuerdo con la experiencia de las características de calidad de la unidad.
Existen dos modelos fundamentales para las gráficas de control:
- Gráfica por mediciones o por “Variables”. La más generalizada de ellas es la gráfica denominada de X, R, S y se emplean cuando se efectúan mediciones.
- Gráfica para datos provenientes de calibradores de pasa-no-pasa o por atributos, empleándose la gráfica de fracción defectuosa o de porcentaje defectuoso (conocidas como las gráficas de p)
Por ejemplo, se supone que se tiene un proceso de fabricación de anillos de pistón para motor de automóvil y a la salida del proceso se toman las piezas y se mide el diámetro. Las mediciones sucesivas del diámetro de los anillos se pueden anotar en una carta como la siguiente:
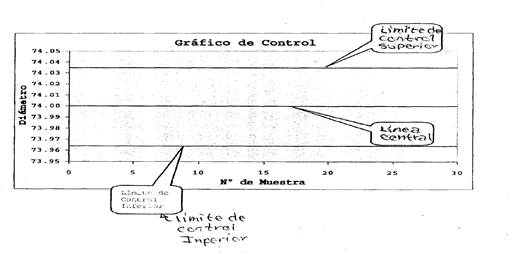
Por ejemplo, si las 15 últimas mediciones fueron las siguientes:
Nº de muestra |
Diámetro |
1 |
74.012 |
2 |
73.995 |
3 |
73.987 |
4 |
74.008 |
5 |
74.003 |
6 |
73.994 |
7 |
74.008 |
8 |
74.001 |
9 |
74.015 |
10 |
74.030 |
11 |
74.001 |
12 |
74.015 |
13 |
74.035 |
14 |
74.017 |
15 |
74.010 |
Entonces tendríamos un gráfico de control como este:
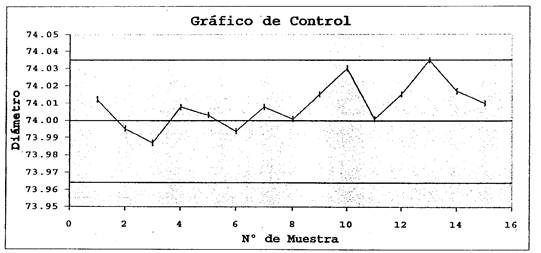
Podemos observar en este gráfico que los valores fluctúan al azar alrededor del valor central (promedio histórico) y dentro de los límites de control superior e inferior. A medida que se fabrican, se toman muestras de los anillos, se mide el diámetro y el resultado se anota en el gráfico, por ejemplo, cada media hora.
Pero ¿Qué ocurre cuando un punto se va fuera de los límites? Eso es lo que ocurre con el último valor en el siguiente gráfico.
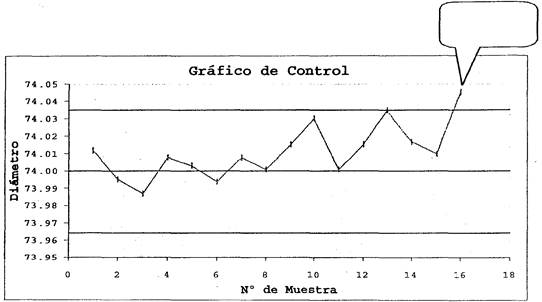
Esa circunstancia puede ser un indicio de que algo anda mal en el proceso. Entonces, es necesario investigar para encontrar el problema (causa asignable) y corregirla. Si no se hace esto el proceso estará funcionando a un nivel de calidad menor que originalmente.
Existe diferentes gráficos X-R, Gráficos C, Gráficos np, Gráficos Cusum, y otros. Cuando se mide una característica de calidad que es una variable continua se utilizan en general los gráficos X-R. Estos en realidad son dos gráficos que reutilizan juntos, el de X (promedio del subgrupo) y el de R (rango del subgrupo). En este caso se toman muestras de varias piezas, por ejemplo 5 y esto es un subgrupo. En cada subgrupo se calcula el promedio X y el rango R (diferencia entre el máximo y el mínimo)
A continuación podemos observar un típico gráfico de X:
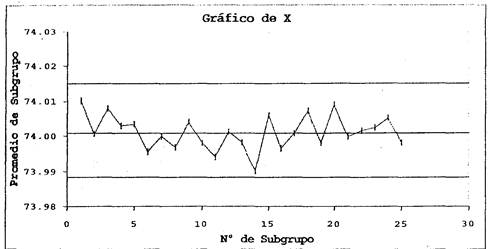
Y lo que sigue es un gráfico de R:
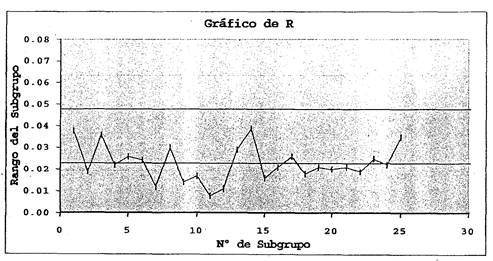
El gráfico de X permite controlar la variabilidad entre los sucesivos subgrupos y el de R permite controlar la variabilidad dentro de cada subgrupo.
10.3 H4 – Diagramas de flujo
Diagrama de flujo es una representación gráfica de la secuencia de etapas, operaciones, movimiento, decisiones y otros eventos que ocurren en el proceso. Esta representación se efectúa a través de formas y símbolos gráficos utilizados usualmente:
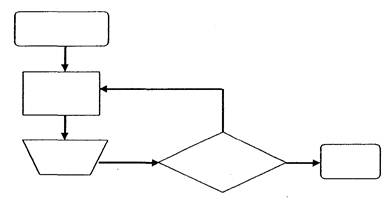
 Los símbolos gráficos para dibujar un diagrama de flujo están más o menos normalizados: Los símbolos gráficos para dibujar un diagrama de flujo están más o menos normalizados:
Símbolo de operación, dentro del cual se hace una breve descripción de la misma
 Símbolo de operación manual. Símbolo de operación manual.
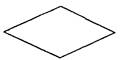 Símbolo de decisión a partir del cual el proceso se bifurca en dos caminos. Símbolo de decisión a partir del cual el proceso se bifurca en dos caminos.
 Símbolo utilizado para marcar el comienzo o el fin de un proceso. Símbolo utilizado para marcar el comienzo o el fin de un proceso.
 Líneas de flujo, que indican el camino que une los elementos del diagrama. Líneas de flujo, que indican el camino que une los elementos del diagrama.
 Símbolo de documento Símbolo de documento
Existen otros símbolos que se pueden utilizar. Lo importante es que su significado se entienda claramente a primera vista. En el ejemplo siguiente, vemos un diagrama de flujo para representar el proceso de fabricación de una resina (reacción de polimerización)
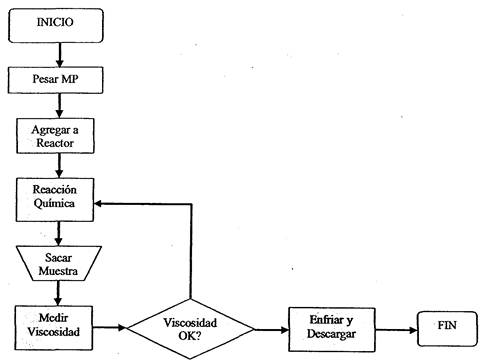
Algunas recomendaciones para construir diagramas de flujo son las siguientes:
- Conviene realizar un diagrama de flujo que describa el proceso real y no lo que está escrito sobre el mismo (lo que se supone debería ser el proceso).
- Si hay operaciones que no siempre se realizan como está en el diagrama, anotar las excepciones en el diagrama.
- Probar el diagrama de flujo tratando de realizar el proceso como está descrito en el mismo, para verificar que todas las operaciones son posibles tal cual figuran en el diagrama.
- Si se piensa en realizar cambios al proceso, entonces se debe hacer un diagrama adicional con los cambios propuestos.
H5 – Histogramas
Un histograma es un gráfico o diagrama que muestra el número de veces que se repiten cada uno de los resultados cuando se realizan mediciones sucesivas. Esto permite ver alrededor de que valor se agrupan las mediciones (tendencia central) y cual es la dispersión alrededor de ese valor central.
Supongamos que un médico dietista desea estudiar el peso de personas adultas de sexo masculino y recopila una gran cantidad de datos midiendo el peso en kilogramos de sus pacientes varones:
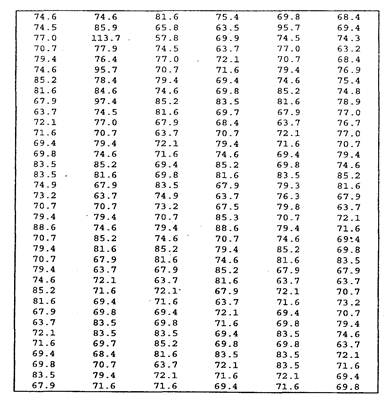
Así como están los datos es muy difícil sacar conclusiones acerca de ellos.
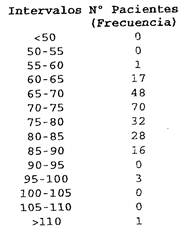
Entonces, lo primero que hace el médico es agrupar los datos en intervalos contando cuantos resultados de mediciones de peso hay dentro de cada intervalo (esta es la frecuencia). Por ejemplo, ¿cuántos pacientes tiene entre 60 y 65kg? ¿Cuántos pacientes tiene entre 65 y 70kg?:
Ahora se pueden representar las frecuencias en un gráfico como el siguiente:
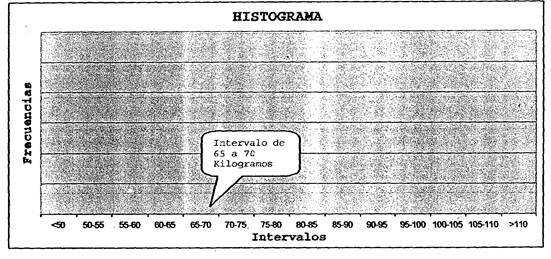
Por ejemplo, la tabla nos dice que hay 48 pacientes que pesan entre 65 y 70 kilogramos. Por lo tanto, levantamos un columna de altura proporcional a 48 en el gráfico:
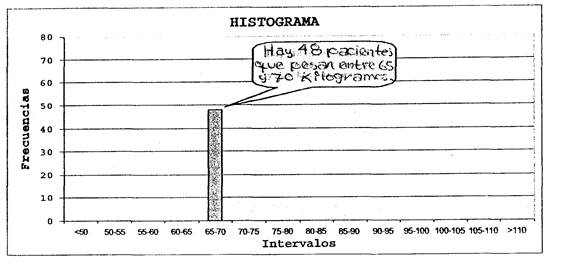
Y agregando el resto de las frecuencias nos queda el histograma siguiente:
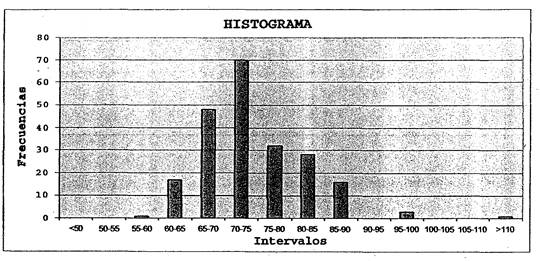
¿Qué utilidad nos representa el histograma? Permite visualizar rápidamente información que estaba oculta en la tabla original de los datos. Por ejemplo, nos permite apreciar que el peso de los pacientes se agrupa alrededor de los 70 – 75 kilos. Esta es la tendencia central de las mediciones. Además podemos observar que los pesos de todos los pacientes están en un rango desde 55 a 100 kilogramos. Esta es la dispersión de las mediciones. También podemos observar que hay muy pocos pacientes por encima de los 90 kilogramos o por debajo de 60 kilogramos.
Ahora el médico puede extraer toda la información relevante de las mediciones que realizó y puede utilizarlas para su trabajo en el terreno de la medicina.
10. 4 H6 – Diagramas de Pareto.
El diagrama de Pareto es un histograma especial, ene. Cual las frecuencias de ciertos eventos aparecen ordenadas de mayor a menor. Vamos a explicarlo con un ejemplo.
Supongamos que un fabricante de heladeras desea analizar cuales son los defectos más frecuentes que aparecen en las unidades al salir de la línea de producción. Para esto, empezó por clasificar todos los defectos posibles en sus diversos tipos:

Posteriormente, un inspector revisa cada heladera a medida que sale de producción registrando sus defectos de acuerdo con dichos tipos.
Después de inspeccionar 88 heladeras, se obtuvo una tabla como está:

La última columna muestra el número de heladeras que presentan cada tipo de defecto, es decir, la frecuencia con que se presenta cada defecto. En lugar de la frecuencia numérica podemos utilizar la frecuencia porcentual, es decir, el porcentaje de heladeras en cada tipo de defecto:

Podemos ahora representar los datos en un histograma como el siguiente:
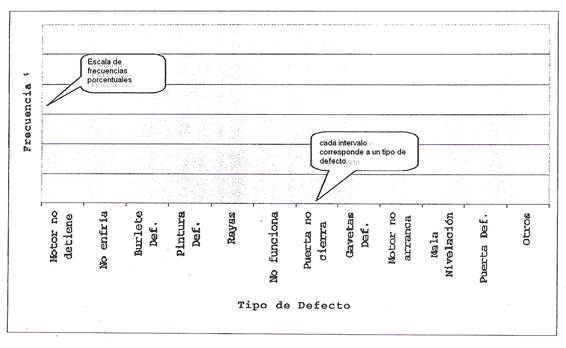
A continuación, en cada intervalo dibujamos una columna de altura proporcional al porcentaje de heladeras que presenta ese tipo de defecto (última columna de la tabla):
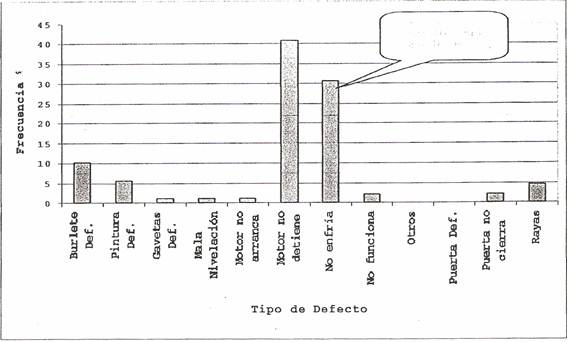
Pero ¿cuáles son los defectos que aparecen con mayor frecuencia? Para hacerlo más evidente, antes de graficar podemos ordenar los datos de la tabla en orden decreciente de frecuencia:

Lo que obtenemos se llama diagrama de Pareto o gráfico de Pareto:
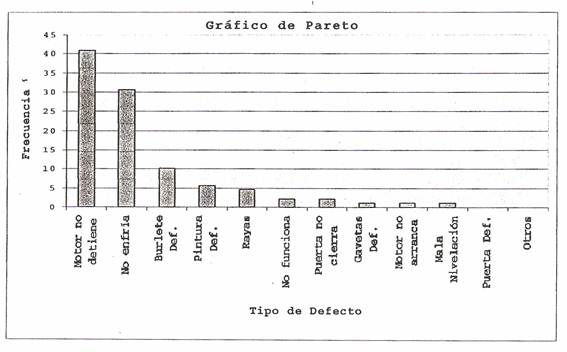
Ahora resulta evidente cuales son los tipos de defectos más frecuentes. Podemos observar que los 3 primeros tipos de defectos se presentan en un 82% de heladeras, aproximadamente. Esto nos conduce a lo que se conoce como principio de Pareto: la mayor de los defectos encontrados en el lote pertenece sólo a 2 ó 3 tipos de defectos, de manera que si se eliminan las causas que los provocan desaparecería la mayor parte de los defectos.
10.5 H7 – Diagramas de dispersión
Los diagramas de dispersión o los gráficos de correlación permiten estudiar la relación entre 2 variables. Dadas 2 variables X e Y, se dice que existe una correlación entre ambas si cada vez que aumenta el valor de X aumenta proporcionalmente el Valor de Y (correlación positiva) o si cada vez que aumenta el valor de X disminuye en igual proporción el valor de Y (correlación negativa).
En un gráfico de correlación representamos cada par por X, Y como un punto donde se cortan las coordenadas de X e Y:
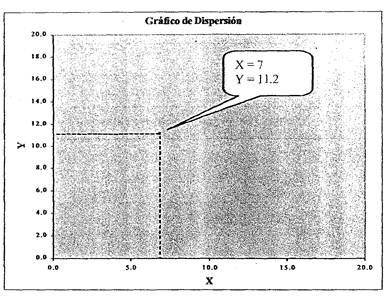
Veamos un ejemplo. Supongamos que tenemos un grupo de personas adultas de sexo masculino. Para cada persona se mide la altura en metros (Variable X) y el peso en kilogramos (Variable Y). Es decir, para cada persona tendremos un par de valores X, Y que son la altura y el peso de dicha persona:
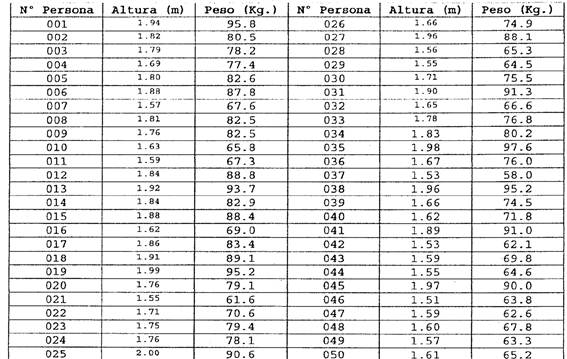
Entonces, para cada persona representamos su altura y su peso con un punto en un gráfico:
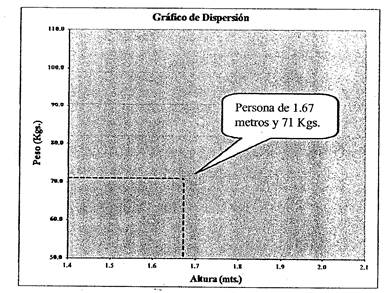
Una vez que representamos a las 50 personas quedará un gráfico como el siguiente:
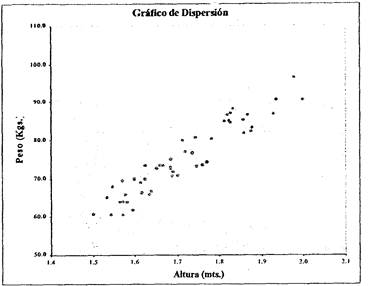
¿Qué nos muestra este gráfico? En primer lugar podemos observar que las personas de mayor altura tienen mayor peso, es decir parece haber una correlación positiva entre altura y peso. Pero un hombre bajito y gordo puede pesar más que otro alto y flaco. Esto es así por que no hay una correlación total y absoluta entre las variables de peso y altura. Para cada altura hay personas de distinto peso:
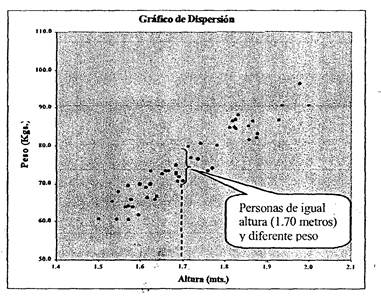
Sin embargo podemos afirmar que existe cierto grado de correlación entre la altura y el peso de las personas.
Cuando se trata de variables cualesquiera, puede no haber ninguna correlación o puede existir alguna correlación en mayor o menor grado, como podemos ver en los gráficos siguientes:
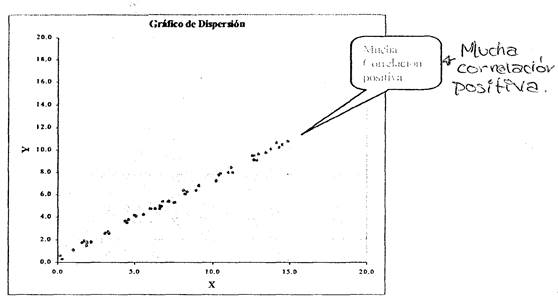
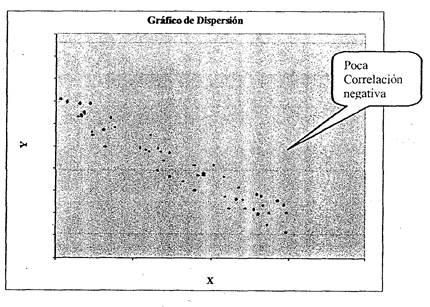
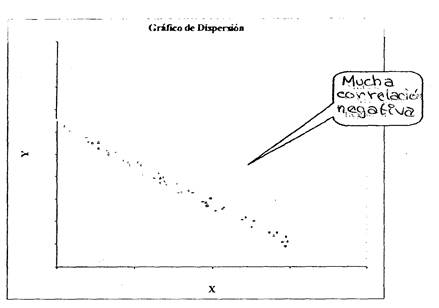
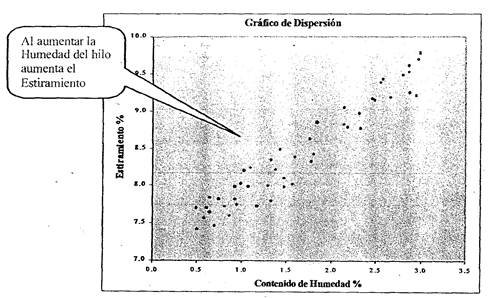
Por ejemplo, en el siguiente gráfico podemos ver la relación entre le contenido de humedad de hilos de algodón y su estiramiento:
|



